The overall process in the electrolysis of water is given by the following molar balance equation (equation 1 ):
The equation is written from left to right, so the reactants are on the left and the products are on the right. This simply states that 1 molecule of water (as liquid) reacts to give 1 molecule of hydrogen (as gas) and 0.5 molecule of oxygen (as gas).
Here we will deal with substances in terms of the kmole (=1000 gram moles), the amount contained in the weight of the material equal to its molecular weight in kg.
Atomic and molecular weights are all relative to an arbitrary reference, the atomic weight of carbon-12, which is defined to have a value of exactly 12. So carbon-12 is the only substance where is atomic weight is an exact number - the atomic weight of anything else is an irrational number (like the value for Pi, it goes on for ever, so we can only ever deal with values to some limiting precision).
Things get a little more complicated because most elements are present in our environment as a mixture of isotopes (same substance, different weight), so for normal hydrogen its atomic weight is 1.007825, but for deuterium (an isotope of hydrogen) the atomic weight is 2.014102. Isotopes differ in weight from one another in units of 1 (roughly) because they differ in the number of neutrons in the atomic nucleus, and neutrons have a relative weight of about 1. Since the typical natural level of deuterium in hydrogen is around 155 ppm (parts per million) the average atomic weight of hydrogen is taken as 1.00784 (it has changed a bit, due to revisions about what the typical level of deuterium is).
Similar considerations apply to oxygen, which has three naturally occurring isotopes with atomic weights of 15.995, 16.999, 17.999 (to the nearest three decimal places); based on proportions of these isotopes the standard oxygen atomic weight is taken to be 15.99903.
The combinations of different hydrogen and oxygen isotopes means that in naturally occurring water we can have water molecules with weights ranging from 18.011 up to 22.027 (though by far the most common value is 18.011).
The values for atomic and standard weights are those published by the International Commission for Pure and Applied Chemistry (IUPAC) and the Commission on Isotope Abundances and Atomic Weights (CIAAW) -
[ see http://www.ciaaw.org and http://www.sbcs.qmul.ac.uk/iupac/AtWt/ ]
Molecular weights can be calculated directly from the constituent atomic weights.
For engineering purposes we can happily use atomic weight values to three decimal places, but rounding errors can still give small apparent inconsistencies in a mass balance, along with additional discrepancies if inconsistent reference data is used.
For example, google ‘molecular weight of water’ and the first number that pops up is 18.01528; whereas the IUPAC standard molecular weight (2015) of water is 18.0147. The difference of 32 ppm is not normally significant, and the two values are the same rounded to 3 decimal places (18.015).
In engineering terms we can happily deal with what is taken as a ‘normal’ mixture of isotopes to represent substances, and use properties derived for that even though different sources can have different isotope ratios (e.g. for water, isotope ratios differ in seawater and rainwater). This arises because the different isotopic combinations behave slightly differently due to the difference in their physical properties. This behaviour can be exploited to separate isotopes. For example, large scale electrolysis can be used to produce deuterium enriched hydrogen.
Some Other Points About Hydrogen Properties
There is another subtlety around the properties of hydrogen. Normal molecular hydrogen (H2) consists of two isomeric forms, para- and ortho- hydrogen, which differ in the alignment of their proton spins. Molecular hydrogen consists of a mixture of the two forms. The equilibrium ratio changes from close to 100% para at very low temperatures and changes with increasing temperature up to the limiting 25%/75% mixture around room temperature. Para and ortho-hydrogen have slightly different properties, so when we consider hydrogen we have to be aware of this.
For gaseous hydrogen at reasonable temperatures we can ignore this effect since the ratio is more or less constant at ambient temperatures and above, and we can deal with the properties of ‘normal’ hydrogen (i.e. the 25/75 para/ortho mixture). However if are dealing with liquefied hydrogen, then we have to be careful. Hydrogen liquefied from room temperatures can still have the ‘normal’ 25/75 para/ortho ratio, and not be in the equilibrium para state. On storage the mixture composition will move towards the equilibrium composition, releasing very significant amounts of heat, similar in magnitude to the latent heat of vapourization. The result is that in cryogenic liquid storage much of the initial hydrogen inventory can boil off due to the change to the para form.
In commercial hydrogen liquefaction catalysts are used to ensure that the liquid is at equilibrium with respect to para/ortho hydrogen and the problem of boil-off doesn’t arise.
However if equilibrated liquid hydrogen is vapourized to feed a fuel cell the material is not ‘normal’ hydrogen but is predominantly para-hydrogen since there is insufficient time for the gas to re-equilibrate at the cell operating temperature. The effect on fuel cell is performance is negligible but the overall system energy balance is significantly impacted.
Energy Changes In Water Electrolysis
In equation at the top the water is specified as being in the liquid state, and the hydrogen and oxygen products as being in the gas state. This is because at room temperature and pressure, these are the normal states of these materials. Here the ‘standard’ conditions (Standard Temperature and Pressure, or STP) are taken as 25C and 1 bara. Be aware however that there are several different definitions of ‘standard’ conditions variously using temperatures of 0C, 20C, 25C (or in the US, even 60F) and pressures of 1 bara or 1 atmosphere (a standard atmosphere is 1.013 bara) .
At standard conditions, the energy input (DH) for equation 1 is 285.8 MJ/kmol.
The electrolysis reaction is simply the reverse of the combustion of hydrogen so as would be expected the splitting of water requires the input of energy. Note that if the reaction as written (left to right) releases energy, the heat of reaction is negative (the reaction is exothermic) if the reaction requires energy input, the heat of reaction is positive (the reaction is endothermic).
When we burn hydrogen (at STP) to produce water, the energy output (the heat of combustion) is simply the negative of the decomposition reaction, or [ -285.8 ] MJ/kmol.
As it happens the standard heat of combustion of hydrogen is also the heat of formation of water.
The heat of formation is defined as the enthalpy change to form the given substance from its elements, those elements being in their standard states. By definition the enthalpy of an element in its standard set is set to zero. That might sound a little odd, but there is no such thing as an absolute enthalpy value, all enthalpies are relative and it is therefore necessary to set an arbitrary reference state; setting all elements to zero is a convenient convention, as it simplifies calculation of any reaction enthalpy change, given the heat of formation for the substances involved.
The heat of combustion value [285.8] is for the product (water) in the liquid state. This is variously termed the Gross Calorific Value (GCV) or Higher Heating Value (HHV).
If the water is instead taken to be in the vapour state, then the heat of combustion is lower by an amount equal to the latent heat of water, giving a value of [241.8] MJ/kmole. This is referred to as the Net Calorific Value (NCV) or Lower Heating Value (LHV). Since many combustion systems do not condense product water, the NCV of a hydrogen containing fuel can be a useful indication of the maximum practical heating value.
We could recover the entire heat of combustion of hydrogen as thermal energy at ambient temperature.
The combustion of hydrogen and oxygen will proceed naturally and inevitably in one direction only. If we want to reverse the process we have to apply at least some of the heat of reaction not as heat, but as work. We cannot drive the reaction in the opposite direction to split water into hydrogen and oxygen simply by heating water at low temperature.
What we have referred to as the ‘heat of reaction’ is more properly the change in the system ‘enthalpy’. The enthalpy change (DH) is only dependent on the initial and final conditions, irrespective of how the reaction is performed.
The minimum amount of input work required for the electrolysis is given by another property of the system, the change in Gibbs Free Energy (DG), named after Willard Gibbs ( see https://en.wikipedia.org/wiki/Josiah_Willard_Gibbs )
At standard conditions, for equation 1: DG = 237.2 MJ/kmol.
We can treat the supply of electricity as being directly equivalent to work, so we can also take this as the minimum electricity requirement for the cell (at standard conditions).
The DG value defines the required electrolysis cell voltage under reversible (i.e. ideal) conditions, where the standard cell voltage (Eo) is given by the Nernst equation:
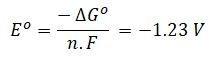
where :
F = Faraday number = 96.485 MJ/V per kmole
n = number of electrons transferred = 2
If we could devise a perfectly reversible electrolysis cell, then the balance of the enthalpy change could be provided by heat (Q), where :
Q = DHo - DGo = 48.6 MJ/kmole
At ambient temperature, at least [237.2/285.8]=83% of the energy required must be in the form of work.
Strictly speaking these energy figures refer to an open cell, where the feed and products are in flow. The calculations do not take into account the actual operating concentration of hydrogen and oxygen in the cell (which will be diluted by the presence of water vapour) and are based on ideal gas behaviour.
In a practical cell factors such as mass transfer limitations, including transport of hydrogen ions across the cell and other effects, mean that the voltage required is higher than the minimum value. The cell efficiency can be defined in terms of the voltage efficiency (e), defined as :
e = standard cell voltage / actual voltage
where a typical value for ‘e ’ is around 70%.
For a cell operating at ambient conditions the power requirement at 70% voltage efficiency would be equivalent to [83%/0.7] = 119% of the required enthalpy input. So inefficiencies mean that there is an excess of heat generated in the cell and a requirement for cell cooling, not cell heating.
The minimum work required reduces as the cell temperature increases. If the cell temperature is increased the minimum work requirement drops. It is this effect that underlies interest in high temperature electrolysis. But there is a twist on this - as the temperature of the heat increases, it has an increasing work equivalence.
Where high temperature heat is available (for example from a nuclear reactor) direct use of the heat rather than using it generate electricity(for example through a steam turbine system) can potentially give a lower overall energy requirement for electrolysis.
Commercial Electrolyzer Technology
There are two commercially available types of water electrolysis technologies:
alkaline electrolysis, typically using potassium hydroxide (KOH) as the electrolyte
PEM electrolyzers, which use a Proton Exchange Membrane (PEM) as a solid electrolyte
The technologies have different characteristics, and previously PEM systems were limited to small capacities but with advancements in technology PEM electrolyzers are now available at large (MW) capacities. Both systems operate at modest temperature (50 to 80C) but PEM electrolyzers can produce hydrogen directly at higher pressure, currently up to around 30 bar.
Manufacturers of electrolysis units include:
PEM type : Siemens, ITM
alkaline type : Hydrogenics, NEL
In alkaline electrolyzers the current through the cell is carried by [OH]- ions whereas in PEM electrolzyers the charge is carried by [H]+ ions. The cell reactions can be written as:
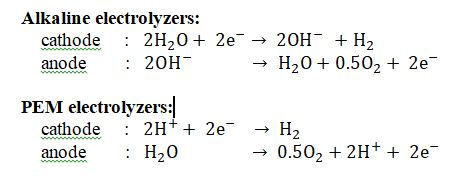
(hence the value of n = 2 , for the calculation of the cell voltage Eo)
Effect of Pressure on Energy Requirement
The energy requirement is impacted by the operating pressure. Producing hydrogen at pressure increases the minimum work requirement since the electrolysis process is in effect compressing the hydrogen up from 1 bara to the designated pressure. For modest pressure the overall enthalpy change is essentially unchanged (since the enthalpy of an ideal gas is not a function of pressure).
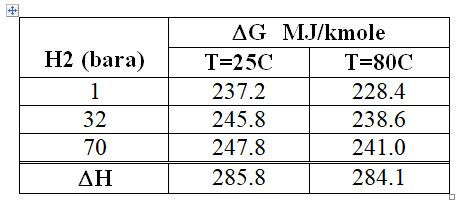
The Gibbs Free Energy change is shown in Table 2 for three values of the hydrogen product pressure, 1 bara (standard conditions), 32 and 70 bara (we will use these numbers later). The heat of reaction (the enthaply change) is also given.
( Figures refer to the system with both reactant and product at either 25C or 80C, 1 bara water and oxygen, hydrogen pressure as specified. Hydrogen and oxygen product taken as the pure components)
Table 2 : Water Decomposition : Effect of H2 Delivery Pressure on DG value


Comments